P.S. Pincushion Priors
So-called “spike-and-slab” models are a prominent choice for prior distributions of parameters in Bayesian analysis,
consisting of a probability “spike” at a value of a priori interest (often a “null” value) and a “slab” distributing
the remaining probability mass across the parameter space.
Rouder and colleagues (2018) provide an excellent
discussion of these archetypal models in Bayesian analysis, and provide a formulation of the spike-and-slab prior using
a Dirac delta “function” to represent the spike as a point mass with infinite probability density.
A neologism for these models which I’ve come up with (and which is original, as far as I can tell from searching
the internet) is that of the “pincushion prior.” The “slab” portion of the prior resembles a pincushion (especially
when convex overall), and the “spike” resembles a pin inserted into the cushion from above. Perhaps this construction
isn’t particularly helpful to anyone, but I find it an accurate (and possibly amusing) portrayal of what a spike-and-slab
prior looks like.
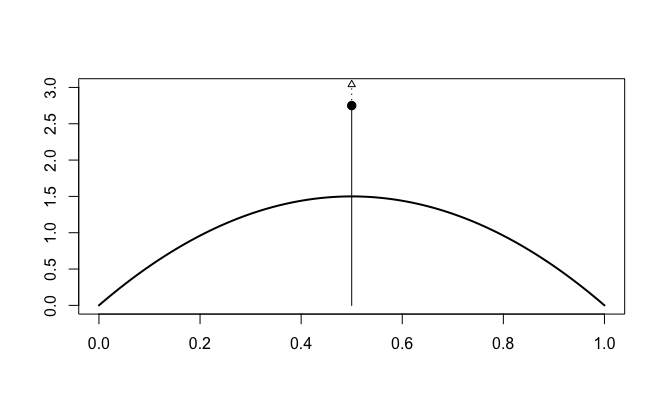
As an example, a convex Beta prior over a parameter space from [0,1] provides a nice pincushion, and a Dirac delta spike at the midpoint provides a nice pin. The illustration is shown below, and (following the notation in Rouder et al., 2018, where
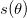 denotes the Dirac delta function and
denotes the Dirac delta function and 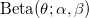 denotes the Beta density) the prior distribution is given as:
denotes the Beta density) the prior distribution is given as:
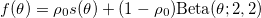
Because the “head” of the pin exists at discrete location above the pincushion, but the spike has infinite density (extending
upward infinitely along the y-axis), I have included a dashed line with an upward-pointing arrow above the head to indicate
this.